A Star GCSE Maths Equivalency Revision
GCSE Equivalency Maths Revision Example Questions
Question 1:
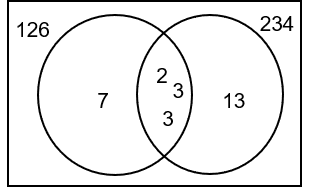
Find the HCF and LCM of 126 and 234.
[4 marks]
126 = 2 \times 3 \times 3 \times 7 = 2 \times 3^2 \times 7
234 = 2 \times 3 \times 3 \times 13 = 2 \times 3^2 \times 13
HCF = 2 \times 3 \times 3 = 18
Found by multiplying the factors from the centre of the Venn diagram.
LCM = 2\times 3 \times 3 \times 7 \times 13 = 1638
Found by multiplying all the factors from the Venn diagram.
Question 2:
Factorise and solve the following quadratic equation: x^2+ 3x - 18=0
[3 marks]
Question 3:
Find the equation of the line AB where, A=(5,10) , B=(11,22).
[3 marks]
m =\dfrac{\text{change in} \, y}{\text{change in} \, x} = \dfrac{22 - 10}{11 - 5} = \dfrac{12}{6} = 2
y = 2x + c
Substituting in values of x and y gives
10 = 2(5) + c
10 = 10 + c
c = 0
So, the equation of the line is:
y = 2x
Question 4:
Terry, Alisha and Ella run on a weekly basis.
In total, they average 176 km a week.
If Alisha runs twice as far as Terry and Ella runs one third of Alisha’s distance, how far do each of them run in km?
[3 marks]
Ratio = Terry : Alisha : Ella = 3:6:2
3 + 6 + 2 = 11
\dfrac{176}{11} = 16
Terry: 16 \times 3 = 48 km
Alisha: 16 \times 6 = 96 km
Ella: 16 \times 2 = 32 km
Question 5:
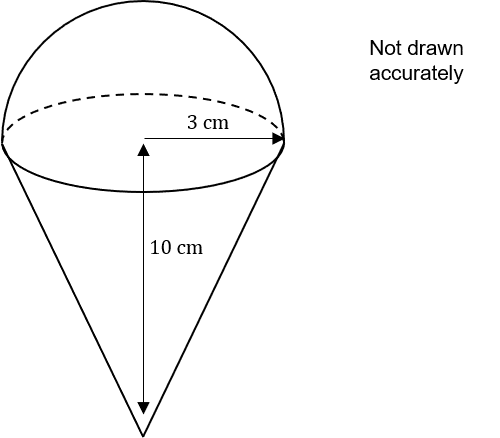
The diagram below shows an ice-cream cone.
This consists of a cone of radius 3 cm and height 10 cm with an attached hemisphere of ice cream of radius 3 cm, as shown below.
Assuming the cone is completely filled, calculate the total volume of ice-cream.
Give your answer in terms of \pi
[5 marks]
Volume of a cone is given by \dfrac{1}{3}\pi r^2h
Substituting in the given values gives the volume of the cone as \dfrac{1}{3}\times \pi \times 3^2 \times 10 = 30\pi cm^3
Volume of a hemisphere is given by \dfrac{1}{2}\times \dfrac{4}{3}\pi r^3 = \dfrac{2}{3}\pi r^3
Substituting in the given values gives the volume of the hemisphere as \dfrac{2}{3}\times \pi \times 3^3 = 18\pi
Adding the two volumes together gives 30\pi + 18\pi = 48\pi cm^3
Question 6:
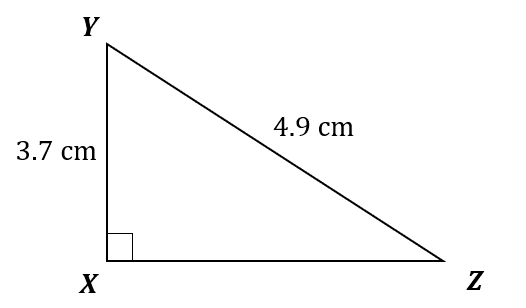
XYZ is a right-angled triangle with
XY = 3.7 cm
YZ = 4.9 cm
Calculate the area of the triangle.
Give your answer correct to 1 decimal place.
[4 marks]
4.9^2 - 3.7^2 = 10.32
\sqrt{10.32} = 3.212... cm
\text{Area} = \dfrac{1}{2} \times 3.7 \times 3.212... = 5.9 cm^2 (1 dp)
Question 7:
a)
The probabilities of a spinner landing on each of its three colours are shown in the table below.
Find the missing value from the table below.
[2 marks]
b)
If the spinner is spun 180 times, how many times would you expect the spinner to land on blue?
[1 mark]
a)
Probabilities add up to 1, so the missing value is
1 - \dfrac{1}{3} - \dfrac{1}{6} = \dfrac{1}{2}
b)
180 \times \dfrac{1}{3} = 60
Question 8:
Calculate (6 \times 10^3) \times (9 \times 10^4) and write the answer in standard form.
[2 marks]
6 \times 9 \times 10^3 \times 10^4 = 54 \times 10^7 = 5.4 \times 10^8
Question 9:
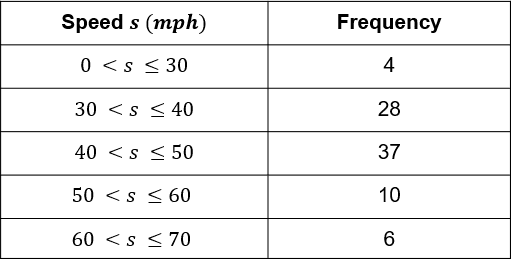
Anna records the speed of cars going past on a busy road.
Use this table to estimate the average speed of the cars.
Give your answer to the nearest whole number.
[4 marks]
(15 \times 4) + (35\times 28) + (45\times 37) + (55\times 10) + (65\times 6) = 60 + 980 + 1665 + 550 + 390 = 3645
n = 4 + 28 + 37 + 10 + 6 = 85
\dfrac{3645}{85} = 42.88... = 43 mph to the nearest whole number
Question 10:
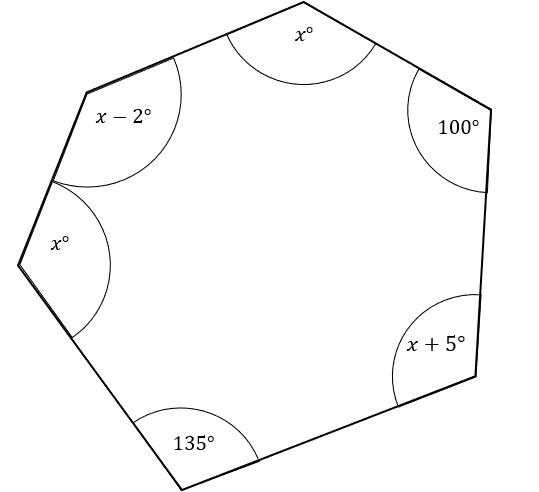
The diagram below shows an irregular hexagon.
Find the value of x to 1 dp
[3 marks]
Using the equation for sum of interior angles
(6-2)\times 180\degree = 720\degree
This is equal to the sum of the given angles, so
x+100+x+5+135+x+x-2=4x+238=720 \degree
Rearranging gives 482=4x
x=120.5\degree